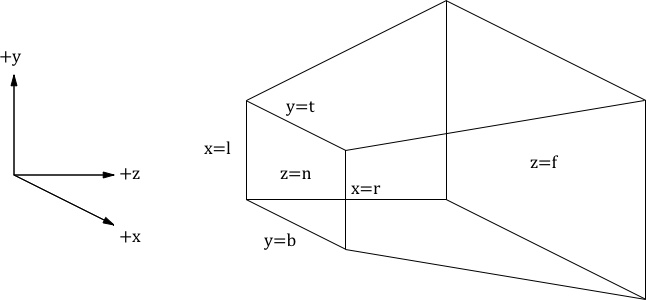
For a perspective projection, we want to map the points inside the view space frustrum to OpenGL NDC (Normalized Device Coordinates) space

The frustrum is defined by
z in [n, f]Where for the near plane
l is the x coordinate of the left bounds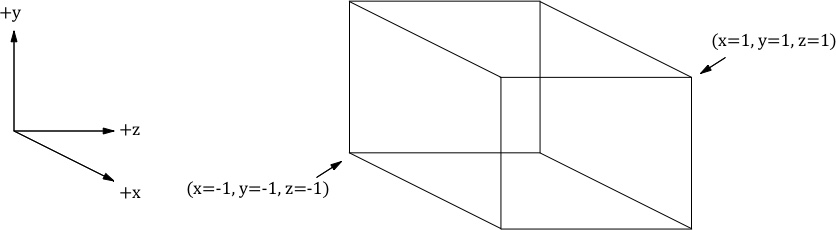
For NDC Space
x in [-1.0, 1.0]For OpenGL, a z coordinate of -1.0 appears in front of a z coordinate of 1.0
For example, if you had a triangle in the xy plane with a constant z of -0.5 it would appear in front of another triangle in the xy plane with a constant z of +0.5
The upper left of the view window corresponds to an xy coordinate of (-1.0, 1.0)
The lower right of the view window corresponds to an xy coordinate of (1.0, -1.0)
Let's map the x coordinates from the frustrum's view space to NDC space
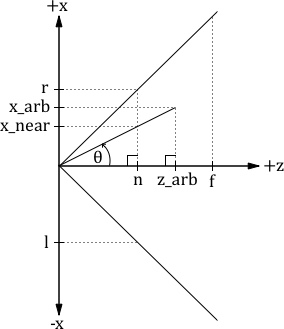
A right triangle is formed by the following three points: the origin at (x=0, z=0), (x=x_near, z=n), and (x=0, z=n)
Another right triangle is formed by the following three points: the origin at (x=0, z=0), (x=x_arb, z=z_arb), and (x=0, z=z_arb)
These are similar triangles
This means that the tan(θ) is equal for both triangles
$${tan(\theta) = {{opposite}\over {adjacent}} = {x_{near}\over n} = {x_{arb}\over z_{arb}}}$$ $${x_{near} = n\cdot{x_{arb}\over z_{arb}}}$$ Remember, for z == nFor z fixed at the near plane, our x coordinate from our graph of the zx slice of the frustrum is x_near
We do a linear mapping for x_near between l and r using the point slope form of a line equation
$${y - y_0 = m\cdot(x - x_0) = \left({y_1 - y_0}\over{x_1 - x_0}\right) \cdot (x - x_0)}$$where (x_0, y_0) is the first point of the line, (x_1, y_1) is the second point of the line, and m is the slope of the line
Our input to the linear mapping is x=x_near, and our output is the x coordinate in NDC space y=x_ndc, whose range is [-1.0, 1.0]
So our input range is [l, r], and the range of our output is [-1.0, 1.0]
Our first point is (x_0=l, y_0=-1.0), and our second point is (x_1=r, y_1=+1.0)
So we have
$${x_{ndc} - (-1.0) = \left({1.0 - (-1.0)}\over{r - l}\right) \cdot (x - l) = \left(2\over{r - l}\right) \cdot \left(n\cdot{x_{arb}\over z_{arb}} - l\right) }$$ $${x_{ndc} + 1 = \left({2}\over{r - l}\right) \cdot \left({{n\cdot x_{arb}}\over z_{arb}} - l\right)}$$ $${x_{ndc} + 1 = {{2n}\over {r - l}} \cdot {x_{arb}\over z_{arb}} - {{2l}\over{r - l}}}$$ $${x_{ndc} = {{2n}\over {r - l}} \cdot {x_{arb}\over z_{arb}} - {{2l}\over{r - l}} - 1 }$$ $${x_{ndc} = {{2n}\over {r - l}} \cdot {x_{arb}\over z_{arb}} - {{2l}\over{r - l}} - {{r-l}\over{r-l}} }$$ $${x_{ndc} = {{2n}\over {r - l}} \cdot {x_{arb}\over z_{arb}} - {\left({{2l}\over{r - l}} + {{r-l}\over{r-l}}\right)} }$$ $${x_{ndc} = {\left({2n}\over {r - l}\right)} \cdot {x_{arb}\over z_{arb}} - {\left({{r + l}\over{r - l}}\right)} }$$Now let's do a similar mapping for the y coordinates from the frustrum's view space to NDC space
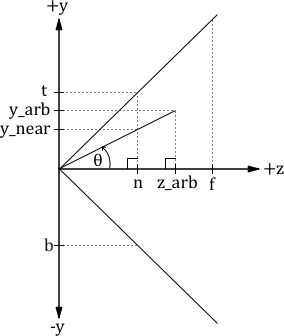
A right triangle is formed by the following three points: the origin at (y=0, z=0), (y=y_near, z=n), and (y=0, z=n)
Another right triangle is formed by the following three points: the origin at (y=0, z=0), (y=y_arb, z=z_arb), and (y=0, z=z_arb)
These are similar triangles
This means that the tan(θ) is equal for both triangles
$${tan(\theta) = {{opposite}\over {adjacent}} = {y_{near}\over n} = {y_{arb}\over z_{arb}}}$$ $${y_{near} = n\cdot{y_{arb}\over z_{arb}}}$$ Remember, for z == nFor z fixed at the near plane, our y coordinate from our graph of the zy slice of the frustrum is y_near
We do a linear mapping for y_near between b and t using the point slope form of a line equation
$${y - y_0 = m\cdot(x - x_0) = \left({y_1 - y_0}\over{x_1 - x_0}\right) \cdot (x - x_0)}$$where (x_0, y_0) is the first point of the line, (x_1, y_1) is the second point of the line, and m is the slope of the line
Our input to the linear mapping is x=y_near, and our output is the y coordinate in NDC space y=y_ndc, whose range is [-1.0, 1.0]
So our input range is [b, t], and the range of our output is [-1.0, 1.0]
Our first point is (x_0=b, y_0=-1.0), and our second point is (x_1=t, y_1=+1.0)
So we have
$${y_{ndc} - (-1.0) = \left({1.0 - (-1.0)}\over{t - b}\right) \cdot (y_{arb} - b) = \left(2\over{t - b}\right) \cdot \left(n\cdot{y_{arb}\over z_{arb}} - b\right) }$$ $${y_{ndc} + 1 = \left({2}\over{t - b}\right) \cdot \left({{n\cdot y_{arb}}\over z_{arb}} - b\right)}$$ $${y_{ndc} + 1 = {{2n}\over {t - b}} \cdot {y_{arb}\over z_{arb}} - {{2b}\over{t - b}}}$$ $${y_{ndc} = {{2n}\over {t - b}} \cdot {y_{arb}\over z_{arb}} - {{2b}\over{t - b}} - 1 }$$ $${y_{ndc} = {{2n}\over {t - b}} \cdot {y_{arb}\over z_{arb}} - {{2b}\over{t - b}} - {{t - b}\over{t - b}} }$$ $${y_{ndc} = {{2n}\over {t - b}} \cdot {y_{arb}\over z_{arb}} - {\left({{2b}\over{t - b}} + {{t - b}\over{t - b}}\right)} }$$ $${y_{ndc} = {\left({2n}\over {t - b}\right)} \cdot {y_{arb}\over z_{arb}} - {\left({{t + b}\over{t - b}}\right)} }$$OpenGL uses 4 dimensional vectors with symbols x, y, z, and w.
x_arb, y_arb, and z_arb are our 3d coordinates of our vertexes that we are doing a perspective projection on. The w_arb coordinate of our vertexes we always set to 1.
$${w_{arb} = 1}$$This 4d space is called "homogeneous space"
The result of the multiplication of our projection matrix by our vertex is a vertex in "clip space"
$${ \begin{bmatrix} m_{00} & m_{10} & m_{20} & m_{30}\\ m_{01} & m_{11} & m_{21} & m_{31}\\ m_{02} & m_{12} & m_{22} & m_{32}\\ m_{03} & m_{13} & m_{23} & m_{33} \end{bmatrix} \cdot \begin{bmatrix} x_{arb}\\ y_{arb}\\ z_{arb}\\ w_{arb} \end{bmatrix} = \begin{bmatrix} x_{clip}\\ y_{clip}\\ z_{clip}\\ w_{clip} \end{bmatrix} }$$OpenGL clips any x_clip, y_clip, or z_clip value that is outside the range [-w_clip, w_clip] to this range
OpenGL then divides the x_clip, y_clip, and z_clip by w_clip to transform from clip space to NDC space
If we cause the value of z_arb to be put into w_clip then in the transform from clip space to NDC space OpenGL will perform an effective divide by z_arb of our x_clip, y_clip, and z_clip
We will then be in 3d OpenGL NDC space, which OpenGL uses to draw with
We know that
$$x_{ndc} = {x_{clip} \over w_{clip}}$$ $$y_{ndc} = {y_{clip} \over w_{clip}}$$ $$z_{ndc} = {z_{clip} \over w_{clip}}$$or
$${x_{clip} = x_{ndc} \cdot w_{clip} = x_{ndc} \cdot z_{arb}}$$ $${y_{clip} = y_{ndc} \cdot w_{clip} = y_{ndc} \cdot z_{arb}}$$ $${z_{clip} = z_{ndc} \cdot w_{clip} = z_{ndc} \cdot z_{arb}}$$So far, we have derived the mapping from Frustrum View Space to NDC Space for x_arb and y_arb
$${x_{ndc} = {\left({2n}\over {r - l}\right)} \cdot {x_{arb}\over z_{arb}} - {\left({{r + l}\over{r - l}}\right)} }$$ $${y_{ndc} = {\left({2n}\over {t - b}\right)} \cdot {y_{arb}\over z_{arb}} - {\left({{t + b}\over{t - b}}\right)} }$$We use these results to get the equations for x_clip and y_clip
$$x_{clip} = {x_{ndc}\cdot z_{arb} = {\left({2n}\over {r - l}\right)} \cdot x_{arb} - {\left({{r + l}\over{r - l}}\right)}\cdot z_{arb} }$$ $$y_{clip} = {y_{ndc}\cdot z_{arb} = {\left({2n}\over {t - b}\right)} \cdot y_{arb} - {\left({{t + b}\over{t - b}}\right)}\cdot z_{arb} }$$We can now fill in some of our projection matrix with what we have derived thus far
$${ \begin{bmatrix} {2n \over {r-l}} & 0 & -{\left(r+l \over r-l\right)} & 0\\ 0 & {2n \over {t-b}} & -{\left(t+b \over t-b\right)} & 0\\ m_{02} & m_{12} & m_{22} & m_{32}\\ m_{03} & m_{13} & m_{23} & m_{33} \end{bmatrix} \cdot \begin{bmatrix} x_{arb}\\ y_{arb}\\ z_{arb}\\ w_{arb}\\ \end{bmatrix} = \begin{bmatrix} x_{clip}\\ y_{clip}\\ z_{clip}\\ w_{clip} \end{bmatrix} }$$We want w_clip = z_arb. We also always set w_arb = 1 for our input vertexes
$${ \begin{bmatrix} {2n \over {r-l}} & 0 & -{\left(r+l \over r-l\right)} & 0\\ 0 & {2n \over {t-b}} & -{\left(t+b \over t-b\right)} & 0\\ m_{02} & m_{12} & m_{22} & m_{32}\\ 0 & 0 & 1 & 0 \end{bmatrix} \cdot \begin{bmatrix} x_{arb}\\ y_{arb}\\ z_{arb}\\ 1\\ \end{bmatrix} = \begin{bmatrix} x_{clip}\\ y_{clip}\\ z_{clip}\\ w_{clip} \end{bmatrix} }$$Now we need to derive an equation for z_clip
We want z_clip to be a linear mapping from z_arb
We do a linear mapping for z_clip using the slope intercept form of a line equation
$${y = {p \cdot x} + q}$$For us, y=z_clip and x=z_arb
$${z_{clip} = {p \cdot z_{arb}} + q}$$We know that z_clip = z_ndc*w_clip
So we have
$${z_{clip} = z_{ndc} \cdot w_{clip}}$$We also know that we are causing z_arb to be put into w_clip so
$${z_{clip} = z_{ndc} \cdot z_{arb} = {p \cdot z_{arb}} + q}$$We know that when z_arb = n that z_ndc = -1.0
$${-1 \cdot n = {p \cdot n} + q}$$ $${-n - pn = q}$$ $${q = -n - pn}$$We know that when z_arb = f that z_ndc = +1.0
$${+1 \cdot f = {p \cdot f} + q = pf + (-n - pn) = p\cdot (f - n) - n}$$ $${(f + n) = p\cdot (f - n)}$$ $${{{f + n}\over {f - n}} = p}$$ $${p = {{f + n}\over {f - n}}}$$Plugging p back into the q equation we find
$${q = -n - pn = -n - \left({{f + n}\over {f - n}}\right) \cdot n = -n\cdot {{f - n}\over {f - n}} -n\cdot {{f + n}\over {f - n}}}$$ $${q = -n\cdot \left({{(f - n) + (f + n)}\over {f - n}}\right) = -n\cdot \left({2f \over {f - n}}\right)}$$ $${q = {-2fn \over {f - n}}}$$So plugging what we've found for p and q into our z_clip equation
$${z_{clip} = {p \cdot z_{arb}} + q = {{f + n}\over {f - n}}\cdot z_{arb} + {-2fn \over {f - n}}}$$Now we can fill out the rest of our projection matrix
$${ \begin{bmatrix} {2n \over (r-l)} & 0 & -{\left(r+l \over r-l\right)} & 0\\ 0 & {2n \over (t-b)} & -{\left(t+b \over t-b\right)} & 0\\ 0 & 0 & {{f + n}\over {f - n}} & {-2fn \over {f - n}}\\ 0 & 0 & 1 & 0 \end{bmatrix} \cdot \begin{bmatrix} x_{arb}\\ y_{arb}\\ z_{arb}\\ 1\\ \end{bmatrix} = \begin{bmatrix} x_{clip}\\ y_{clip}\\ z_{clip}\\ w_{clip} \end{bmatrix} }$$